16.1E: Exercises for Section 16.1 (2024)

1. The domain of vector field \(\vecs{F}=\vecs{F}(x,y)\) is a set of points \((x,y)\) in a plane, and the range of \(\vecs F\) is a set of what in the plane?

Answer

Vectors

For exercises 2 - 4, determine whether the statement is true or false.

2. Vector field \(\vecs{F}=⟨3x^2,1⟩\) is a gradient field for both \(ϕ_1(x,y)=x^3+y\) and \(ϕ_2(x,y)=y+x^3+100.\)

3. Vector field \(\vecs{F}=\dfrac{⟨y,x⟩}{\sqrt{x^2+y^2}}\) is constant in direction and magnitude on a unit circle.

Answer

False

4. Vector field \(\vecs{F}=\dfrac{⟨y,x⟩}{\sqrt{x^2+y^2}}\) is neither a radial field nor a rotation field.

For exercises 5 - 13, describe each vector field by drawing some of its vectors.

5. [T] \(\vecs{F}(x,y)=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}\)

Answer

6. [T] \(\vecs{F}(x,y)=−y\,\hat{\mathbf i}+x\,\hat{\mathbf j}\)

Answer

7. [T] \(\vecs{F}(x,y)=x\,\hat{\mathbf i}−y\,\hat{\mathbf j}\)

Answer

8. [T] \(\vecs{F}(x,y)=\,\hat{\mathbf i}+\,\hat{\mathbf j}\)

9. [T] \(\vecs{F}(x,y)=2x\,\hat{\mathbf i}+3y\,\hat{\mathbf j}\)

Answer

10. [T] \(\vecs{F}(x,y)=3\,\hat{\mathbf i}+x\,\hat{\mathbf j}\)

Answer

11. [T] \(\vecs{F}(x,y)=y\,\hat{\mathbf i}+\sin x\,\hat{\mathbf j}\)

Answer

12. [T] \(\vecs F(x,y,z)=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}+z\,\hat{\mathbf k}\)

13. [T] \(\vecs F(x,y,z)=2x\,\hat{\mathbf i}−2y\,\hat{\mathbf j}−2z\,\hat{\mathbf k}\)

Answer

14. [T] \(\vecs F(x,y,z)=yz\,\hat{\mathbf i}−xz\,\hat{\mathbf j}\)

For exercises 15 - 20, find the gradient vector field of each function \(f\).

15. \(f(x,y)=x\sin y+\cos y\)

Answer

\(\vecs{F}(x,y)=\sin(y)\,\hat{\mathbf i}+(x\cos y−\sin y)\,\hat{\mathbf j}\)

16. \(f(x,y,z)=ze^{−xy}\)

17. \(f(x,y,z)=x^2y+xy+y^2z\)

Answer

\(\vecs F(x,y,z)=(2xy+y)\,\hat{\mathbf i}+(x^2+x+2yz)\,\hat{\mathbf j}+y^2\,\hat{\mathbf k}\)

18. \(f(x,y)=x^2\sin(5y)\)

19. \(f(x,y)=\ln(1+x^2+2y^2)\)

Answer

\(\vecs{F}(x,y)=\dfrac{2x}{1+x^2+2y^2}\,\hat{\mathbf i}+\dfrac{4y}{1+x^2+2y^2}\,\hat{\mathbf j}\)

20. \(f(x,y,z)=x\cos\left(\frac{y}{z}\right)\)

Answer

\(\vecs \nabla f(x,y,z)=\langle \cos(\frac{y}{z}), \,\frac{-x}{z}\sin(\frac{y}{z}), \,\frac{xy}{z^2}\sin(\frac{y}{z})\rangle\)

21. What is vector field \(\vecs{F}(x,y)\) with a value at \((x,y)\) that is of unit length and points toward \((1,0)\)?

Answer

\(\vecs{F}(x,y)=\dfrac{(1−x)\,\hat{\mathbf i}−y\,\hat{\mathbf j}}{\sqrt{(1−x)^2+y^2}}\)

For exercises 22 - 24, write formulas for the vector fields with the given properties.

22. All vectors are parallel to the \(x\)-axis and all vectors on a vertical line have the same magnitude.

Answer

\(\vecs{F}(x,y)=x\,\hat{\mathbf i}+0\,\hat{\mathbf j}\)

23. All vectors point toward the origin and have constant length.

Answer

\(\vecs{F}(x,y)=\dfrac{(y\,\hat{\mathbf i}−x\,\hat{\mathbf j})}{\sqrt{x^2+y^2}}\)

24. All vectors are of unit length and are perpendicular to the position vector at that point.

25. Give a formula \(\vecs{F}(x,y)=M(x,y)\,\hat{\mathbf i}+N(x,y)\,\hat{\mathbf j}\) for the vector field in a plane that has the properties that \(\vecs{F}=\vecs 0\) at \((0,0)\) and that at any other point \((a,b), \vecs F\) is tangent to circle \(x^2+y^2=a^2+b^2\) and points in the clockwise direction with magnitude \(\|\vecs F\|=\sqrt{a^2+b^2}\).

Answer

\(\vecs{F}(x,y)=y\,\hat{\mathbf i}−x\,\hat{\mathbf j}\)

26. Is vector field \(\vecs{F}(x,y)=(P(x,y),Q(x,y))=(\sin x+y)\,\hat{\mathbf i}+(\cos y+x)\,\hat{\mathbf j}\) a gradient field?

Answer

Yes since Py = Qx

27. Find a formula for vector field \(\vecs{F}(x,y)=M(x,y)\,\hat{\mathbf i}+N(x,y)\,\hat{\mathbf j}\) given the fact that for all points \((x,y)\), \(\vecs F\) points toward the origin and \(\|\vecs F\|=\dfrac{10}{x^2+y^2}\).

Answer

\(\vecs{F}(x,y)=\dfrac{−10}{(x^2+y^2)^{3/2}}(x\,\hat{\mathbf i}+y\,\hat{\mathbf j})\)

For exercises 28 - 29, assume that an electric field in the \(xy\)-plane caused by an infinite line of charge along the \(x\)-axis is a gradient field with potential function \(V(x,y)=c\ln\left(\frac{r_0}{\sqrt{x^2+y^2}}\right)\), where \(c>0\) is a constant and \(r_0\) is a reference distance at which the potential is assumed to be zero.

28. Find the components of the electric field in the \(x\)- and \(y\)-directions, where \(\vecs E(x,y)=−\vecs ∇V(x,y).\)

29. Show that the electric field at a point in the \(xy\)-plane is directed outward from the origin and has magnitude \(\|\vecs E\|=\dfrac{c}{r}\), where \(r=\sqrt{x^2+y^2}\).

Answer

\(\|\vecs E\|=\dfrac{c}{|r|^2}r=\dfrac{c}{|r|}\dfrac{r}{|r|}\)

A flow line (or streamline) of a vector field \(\vecs F\) is a curve \(\vecs r(t)\) such that \(d\vecs{r}/dt=\vecs F(\vecs r(t))\). If \(\vecs F\) represents the velocity field of a moving particle, then the flow lines are paths taken by the particle. Therefore, flow lines are tangent to the vector field.

For exercises 30 and 31, show that the given curve \(\vecs c(t)\) is a flow line of the given velocity vector field \(\vecs F(x,y,z)\).

30. \(\vecs c(t)=⟨ e^{2t},\ln|t|,\frac{1}{t} ⟩,\,t≠0;\quad \vecs F(x,y,z)=⟨2x,z,−z^2⟩\)

31. \(\vecs c(t)=⟨ \sin t,\cos t,e^t⟩;\quad \vecs F(x,y,z) =〈y,−x,z〉\)

Answer

\(\vecs c′(t)=⟨ \cos t,−\sin t,e^{−t}⟩=\vecs F(\vecs c(t))\)

For exercises 32 - 34, let \(\vecs{F}=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}\), \(\vecs G=−y\,\hat{\mathbf i}+x\,\hat{\mathbf j}\), and \(\vecs H=x\,\hat{\mathbf i}−y\,\hat{\mathbf j}\). Match \(\vecs F\), \(\vecs G\), and \(\vecs H\) with their graphs.

32.

33.

Answer

\(\vecs H\)

34.

For exercises 35 - 38, let \(\vecs{F}=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}\), \(\vecs G=−y\,\hat{\mathbf i}+x\,\hat{\mathbf j}\), and \(\vecs H=−x\,\hat{\mathbf i}+y\,\hat{\mathbf j}\). Match the vector fields with their graphs in (I)−(IV).

1. \(\vecs F+\vecs G\)
2. \(\vecs F+\vecs H\)
3. \(\vecs G+\vecs H\)
4. \(−\vecs F+\vecs G\)

35.

Answer

d. \(−\vecs F+\vecs G\)

36.

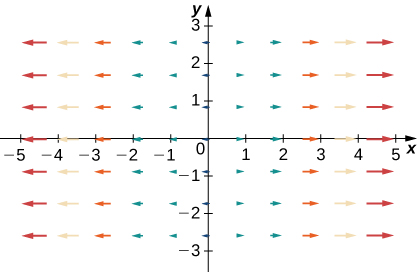
37.

Answer

a. \(\vecs F+\vecs G\)

38.